Assignment 4-Hypothesis Testing
Goals of Assignment 4
Distinguish Between a Z- and T-Test
Calculate a z and t test
Use the Steps of Hypothesis Testing
Make Decisions About the Null and Alternative Hypotheses
Utilize Real-world Data Connecting Stats and Geography

Introduction

T-Tests: T-tests are used to test the mean of a sample population against a mean of a hypothesized population to determine if there is a difference. T-tests are used when you do not know the hypothesized population's standard deviation and when the sample population's size less than 30. 
The t-test tests whether the samples form a normal distribution or not and is based on Degrees of Freedom (the number of observations n-1, which is the degree to which a calculated statistic can vary).

Z-Test: Z-tests are similar but are used when the sample population's size is greater than 30 and the hypothesized population's standard deviation is known. The z-test is based on a sample that has a normal distribution.     

Hypothesis Testing Steps

State the Null: The null hypothesis is that of no difference, that there is no difference between the sample and hypothesized means.

State the Alternative Hypothesis: The alternative hypothesis is that of difference, that there is a difference between the sample and hypothesized means.

Choose a Statistical Test: In this assignment, we choose between the t- and z-tests, which are dependent upon sample sizes.

Set the Significance: The significance level is the probability of a Type I Error occurring. A Type 1 error is when we reject the null when we should not (a false positive). Significance can be set at any level you choose, but the usual levels of significance are 95% and 99%. This means that there is either a 95% or 99% chance that a Type I error will not occur.It also means that the calculated statistic would result in a false positive 5 or 1 times out of 100. These tests are either one-tailed or two-tailed. We use a two-tailed test when direction is not known and a one-tailed when direction or standard is given. When using a two-tailed the probability of a Type I Error occurring (5 times for a 95% significance level) will be divided in half. So, a 95% significance level would be set at 2.5% at both the left and ride sides of the distribution curve. A degrees of freedom and z-score chart are used to determine critical values.

Calculate Test Statistic: The equations used for this assignment are presented in Figures 3 and 4. A sample calculation of a t-value is in the ground nuts example, step 5. As you can see the formulas are identical.

Make a Decision Regarding the Null Hypothesis: Our degrees of freedom and significance levels determine our Critical Intervals and Critical Values. Critical Intervals are the range of numbers that fall between significance levels. For example, if our calculated statistic falls in this range we fail to reject the null as there is no difference. The opposite is true; if the calculated statistic falls outside of this range we would reject the null as there is a difference. The Critical Value is the "cutoff" value in that these are the numbers on each end of the critical intervals. Figure 1 portrays these ideas; the z-stat of 2.2 falls outside of our critical value so we would reject the null in this case.    

Figure 1: Critical Values and Intervals

(Ryan Weichelt)

Part I: T and Z Tests

1.

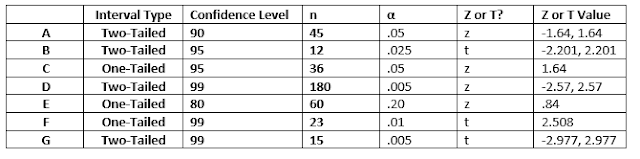
Figure 2: Z and T Test Exercise Results

2. A Department of Agriculture and Live Stock Development organization in Kenya estimates that yields in a certain district should approach the following amounts in metric tons (averages based on data from the whole country) per hectare: groundnuts. 0.55; cassava, 3.8; and beans, 0.28.  A survey of 23 farmers had the following results:

Figure 3: Data Table of Farmer Showing Sample Mean, µ, and Hypothesized Mean, µh.

Ground Nuts

1. State the Null: There is no difference between the farmer sample mean and national mean in ground nut production.

2. State the Alternative Hypothesis: There is a difference between the farmer sample mean and national mean in ground nut production.

3. Choose Statistical Test: As n<30, a two-tailed t-test will be used. Will be used for entire problem and will not be listed separately for the cassava or beans problems. 

4. Set Significance Level: Significance level is set to 95% for these analyses. With degrees of freedom equal to 22 and a two-tailed test,  the critical values will be -2.074 and 2.074 will be used for entire problem and will not be listed separately for the cassava or beans problems.

5. Calculate Test Statistic: 

Figure 4: T-Test Equation

(Ryan Weichelt)

Using the formula (Figure 4) and the data found on Figure 3 and an n of 23, the calculation resulted in a t-statistic of -.6667, after performing the following operations: .51-.55, divided by .3/square root of 23. This is used for the initial problem only as an example.

6. Make Decision Regarding the Null Hypothesis: In this case, we fail to reject the null as our calculated t-statistic did not exceed the critical values of -2.074 and 2.074. There is no difference between the sample mean (farmer survey sample mean) and the hypothesized mean (national production mean).

Probability Value of Calculated Answer: The probability of this calculated value is 0.75400, or 75.4%. The probability is 2.5%, so the null hypothesis was not rejected as 24.6% is greater than 2.5%.

Cassava 

1. State the Null Hypothesis: There is no difference between the farmer sample mean and the national mean in cassava production. 

2. State the Alternative Hypothesis: There is a difference between the farmer sample mean and the national mean in cassava production.

3. Calculate Test Statistic: This calculation resulted in a t-statistic of -2.667, using data found on Figure 1 and the formula in Figure 2, with an n of 23. 

4. Make Decision Regarding the Null Hypothesis: In this case we reject the null as our calculated 

t-statistic exceeded the critical values of -2.074 and 2.074. There is a difference between the sample mean (farmer survey sample mean) and hypothesized mean (national production mean).

Probability Value of Calculated Answer: The probability of this calculated value is .99311, or 99.311%. The probability is 2.5%, so the null hypothesis was rejected as .689% is less than 2.5%.

Beans

1. State the Null Hypothesis: There is no difference between the farmer sample mean and the national mean in bean production.

2. State the Alternative Hypothesis: There is a difference between the farmer sample mean and the national mean in bean production.

3. Calculate Test Statistic: This calculation resulted in a t-statistic of 1.6667 using the data found on Figure 1 and the formula in Figure 2, with an n of 23.

4. Make Decision Regarding the Null Hypothesis: In this case, we fail to reject the null hypothesis as our calculated t statistic did not exceed the critical values of -2.074 and 2.074. There is no difference between the sample mean (farmer survey sample mean) and hypothesized mean (national production mean).

Probability Value of Calculated Answer: The probability of this calculated value is .94768, or 94.768%. The probability is 2.5%, so the null hypothesis was not rejected as 5.23% is greater than 2.5%.

Results

According to the t-tests performed, the sample farm's production of beans and ground nuts was not statistically different than the national production mean for these products. There was, however, a statistically significant difference in cassava production; the sample's mean was lower than the national mean. The t-tests tells us that there is a difference here but does explain what that difference is. The sample means for ground nuts and cassava were both below the national production mean but only cassava was statistically significant. The sample mean was higher than the national mean for beans production but was not found to be statistically significant.

3. A researcher suspects that the level of a particular stream’s pollutant is higher than the allowable limit of 4.4 mg/l.  A sample of n= 17 reveals a mean pollutant level of 6.8 mg/l, with a standard deviation of 4.2.  What are your conclusions?  (one tailed test, 95% Significance Level) Please follow the hypothesis testing steps.  What is the corresponding probability value of your calculated answer.

1. Null Hypothesis: There is no difference between the sampled stream's mean pollutant level and the allowable limit.

2. Alternative Hypothesis: There is a difference between the sampled stream's mean pollutant level and the allowable limit.

3. Choose Statistical Test: As n<30 a t test will be used (Figure 1). 

4. Set Significance Level: Significance is set at 95%, one-tailed test as there is a set standard for pollutant levels. The critical value for this test with 16 degrees of freedom is 1.746.

5. Calculate the Statistic: This calculation resulted in a t statistic of  2.355.

6. Make Decision Regarding the Null Hypothesis: Based on our calculated t statistic of 2.355 we will reject the null as this observed value exceeds the critical value of 1.746. There is a difference between the sample mean (stream samples) and the hypothesized mean (allowable limit of pollutants in streams).

Probability Value of Calculated Answer: The probability of this calculated value is 0.98660, or 98.66%. The probability is 5%, so the null hypothesis was rejected as 1.34% is less than 5%. 

Part II: Utilizing Real-World Data Connecting Statistics and Geography

1. State The Null Hypothesis: There is no difference between the sample mean, home values in the City of Eau Claire, and the hypothesized mean, home values in Eau Claire County outside of the city of Eau Claire.

2. State the Alternative Hypothesis: There is a difference between the sample mean, home values in the City of Eau Claire, and the hypothesized mean, home values in  Eau Claire County outside of the city of Eau Claire.

3. Choose Statistical Test: As n>30, a z-test will be used to calculate this statistic. The critical values for this test is -1.96 and 1.96..

4. Choose Significance Level: The significance level is set at 95%; a two-tailed test is used as the direction is unknown.

5. Calculate Test Statistic: 

Figure 5: Z-test Equation

(Ryan Weichelt)

The overall mean home values in Eau Claire County by block group is $169,438 (hypothesized mean) and the mean home values in the city of Eau Claire by block group is $151,876 (sample mean).The standard deviation for our sample is 49,706.9 and the number of observations in our sample is 53. This resulted in a z-statistic of -2.57 using the equation in Figure 5. 

6. Make a Decision Regarding the Null Hypothesis: As our calculated z-statistic falls below our critical valule of -1.96, we reject the null hypothesis.

Probability Value of Calculated Answer: The probability of this calculated value is .9949, or 99.49%. The probability is 2.5%, so the null hypothesis was rejected as .51% is less than 2.5% 

Results 

It was found that home values in the city of Eau Claire are significantly lower than Eau Claire County as a whole. As can be seen in Figure 5, the lowest values are all located within the city limits of Eau Claire (upper northwest corner with black border). The homes with the lowest values are located near the center and north of the center of the city, with more valuable homes being located on the outer edges of the city limits. No average home values outside of the city of Eau Claire are below $122,260. Figure 6 shows the same information but is presented using the Standard Deviation classification method. Most of the block groups with a negative standard deviation are located within the City of Eau Claire's limits, with values approaching -1.5 standard deviations from the mean in 3 areas. This means that they are further from the mean on the negative standard deviation side and have lower average values. The calculated z-statistic tells us that there is a difference but does not explain what that difference is. Several interesting questions could be asked. Are lot sizes larger outside of the city, on average? Is there a difference in size between homes in Eau Claire and the rest of the county, on average? Do "bad neighborhoods" have an influence on values? How many homes are in each block group? These questions are simple but, given more data, are easily answerable. There are several other questions that could be asked but would require more than a z-score to answer, such as "Do the location city dumps, waste treatment plants, or industrial areas affect average home values as a function of distance?"

Figure 5: Average Home Values in Eau Claire County

Figure 6: Average Home Values in Eau Claire County, Standard Deviation Classification Method