Assignment 3

Goals of Assignment 3

Add a Field in ArcMap

Calculate Z-Scores From Data in ArcMap

Use Probability to Predict Occurrences of a Given Percentage

Create a Report Connecting all of the Data

Introduction

Foreclosures are "the action of taking possession of a mortgaged property when the mortgagor fails to keep up their mortgage payments" (Google Dictionary), and this spatial analysis is being conducted as a response to an increasing concern among Dane County officials due to increasing foreclosure numbers in the county. A census tract are "small, relativity permanent statistical subdivisions of a county, uniquely numbered with a numeric code" (United States Census Bureau) and average about 4,000 people per tract. The purpose of this project is to determine the z-scores of three census tracts, to determine the number of foreclosures that have an 80% and 10% likelihood of occurring, to determine whether the number of foreclosures will increase in 2013, and to perform a spatial analysis to determine changing patterns in foreclosures by census tract in Dane County, Wisconsin, from 2011-2012.

Methodology

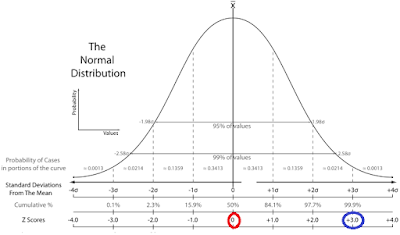
To determine z-scores, the probability of an increase in foreclosures in 2013, and the spatial relationship of foreclosures in Dane County between the years 2011 and 2012, three operations were performed: a hand calculation of z-scores, a hand calculation of the probability of an increase in foreclosures in 2013, and a spatial analysis of foreclosure data mapped using ArcMap. A z-score is simply the distance, in standard deviations, above or below the mean that a raw score falls on, as seen in Figure 1 (two example z-scores circled in red and blue) which allows us to explain the probability of an observation occurring. Z-scores of census tracts 25, 108, and 120.01 were calculated using data for 2011 and 2012, while the probability of an increase in foreclosures used 2012 foreclosure data exclusively. The formula used to calculate z-scores and probability is shown in Figure 2, where z is the z-score, X is observation, μ is the mean, and σ is the standard deviation for this data set. The observation, mean, and standard deviations data were found using ArcMap classification statistics. The final task was mapping the changes in foreclosures for the entirety of Dane County. A new field was added in ArcMap, named change, representing the difference (positive or negative) in the number of foreclosures observed between 2011 and 2012. Another chloropleth map was then created using the Count2012 data that comprises the total number of foreclosures in Dane County in 2012 (Figure 6). Two additional maps (Figures 7 and 8), using the Count2011 and Count2012 data columns in ArcMap, were then created in ArcMap and displayed the total number of foreclosures using the standard deviation classification method. This allowed for a connection between z-score calculation in census tracts 25, 108, and 120.01 and the data displayed on these maps. The 2011 foreclosure map portrayed the data in four standard deviation classes while the 2012 foreclosure map portrayed the data in five standard deviation classes. All analyses utilized information provided by Dr. Ryan Weichelt and consisted of geocoded addresses of disclosures and all census tracts that contain these addresses in Dane County and a z-score chart (Figure 3). 

Figure 1: Normal Distribution with Z-Score Distribution    

(http://www.statisticshowto.com/when-to-use-a-t-score-vs-z-score/)

Figure 2: Z-Score Formula
(https://openlab.citytech.cuny.edu/2013-spring-mat-1272-reitz/2013/05/page/2/) 

Figure 3: Z-Score Chart

Results

The z-scores for census tracts 25, 108, and 120.1 were calculated (using Figures 2 and 3) and the results are portrayed in Figure 4. In 2011 the mean number of foreclosures in Dane County census tracts was 11.39 while the standard deviation was 8.78. Census tracts 108 and 120.01 both have more foreclosures than the mean whereas census tract 25 falls below the mean (Figure 7). These z-score values change when looking at the 2012 data (Figures 4 and 8). The mean increased to 12.3 (due to an overall increase in the number of foreclosures in 2012 over 2011) and the standard deviation  increased to 9.9, reflecting a slight spreading of data about the mean. Census tract 25 moves farther from the mean, reflecting a decrease in foreclosures, census tract 108 moves closer to the mean, also representing a decrease in foreclosures, while 120.01 increases drastically so that it is now 3 standard deviations from the mean (Figure 8). The number of foreclosures that is likely 80% of the time is 3.98 while the number that is likely 10% of the time is 24.97 (Figure 4). Figure 5 represents the total changes in the number of foreclosures in census tracts between 2011-2012 using the Jenks Natural Breaks classification method. There was an overall increase in foreclosures in Dane County from 2011-2012 ((evidenced by the increase in mean mentioned previously), but this increase is not distributed evenly among the census tracts and a spatial pattern emerges. The highest numbers of observed increases (11-16), occurred in seven census tracts (including census tract 120.01) on or near the outer edges of Dane County, primarily in the east. More moderate increases (1-9) occurred in or near the center of the county and on the western edge of Dane County. Decreases in foreclosure rates were most pronounced (-14--6) in census tracts 120.02 and 132 (among others) and all decreases generally run along a line running northeast to southwest from census tract 117 to census tract 126. Using Figure 5, we observe that census tracts 25 and 108 had 2-5 less foreclosures in 2012 while census tract 12.01 had 11-16 more foreclosures. Figures 7 and 8 portray the total number of foreclosures using the standard deviation classification method by year. These maps, used in conjunction, show that the center of Dane County is generally below the average number of foreclosures per census tract, a higher than average south of the center of the county, and that the eastern and northern boundaries have a higher than average number of foreclosures. Figure 6 represents the spatial distribution of the total number of foreclosures in Dane County in 2012. Figure 6 has a spatial pattern that matches Figure 5 in several ways, including a generally low number of foreclosures in census tracts running from the northeast to the southwest, with a very low number of foreclosures located in the center of Dane County, and higher numbers observed along the eastern and northern edges of Dane County. Figure 6 can be used in conjunction with Figure 5 in determining where we observe the greatest increases in the number of foreclosures between 2011-2012 (Figure 5) and where the number of foreclosures is the greatest in 2012 (Figure 6). Census tracts 116, 120.01, and 119 are among those that fit these criteria. Census tracts 114.01 and 114.02, while having high numbers of foreclosures in 2012, have not experienced as high of an increase compared to the tracts mentioned in the preceding sentence, and, therefore, do not fit with the criteria that has been set by the author (which can be adjusted; see conclusion).  

Conclusion

The results show that not all census tracts are experiencing high numbers of foreclosures or an increase in foreclosures. There is a pattern of higher than average foreclosures on the northern and eastern boundaries of the county and south of Dane County's center. Lower than average foreclosures are generally found in the center of the county and to the immediate east of the county center. These findings are significant as that they can be used to guide county officials to where help may be most needed. Recommendations will be made to county officials that several census tracts, including tracts 116, 120.01, and 119, should be of immediate concern as they have had large increases between 2011-2012 along with high total foreclosures in 2012. A focus has been limited to counties that have a high number of foreclosures in 2012 and high increases from 2011-202 as county resources may not be able to effectively help and support numerous families with things such as financial aid, temporary housing, or nutritional needs. If there are enough county resources, an exception could be made. Some census tracts, such as tract 129 (Figure 6), have gone from low single to double digits in one year (2 to 16 in census tract 129's case), or have a high overall number of foreclosures, such as that observed in census tracts 114.01 and 114.02 (Figure 6). The reason for the increase in foreclosures is not known as limited data was utilized answering the study questions but it would be fair to assume that an increase in the number of foreclosures would be observed in 2013 for the following reasons: we observe an increase in total foreclosures from 2011-2012, which could suggest a trend, an economic downturn could occur resulting in even more foreclosures, the standard deviation map of 2012 (Figure 8) has an additional class that is >2.5 standard deviations from the mean, containing 3 census tracts, which is unlikely if the number of foreclosures observed is simply due to chance (3/106 or 2.8% against 1.6% expected, Figure 1). We also have a positively skewed distribution (as evidenced by the lower than expected standard deviation values on the left,<-0.5, of the curve as compared to higher than expected values on the right, >2.5) as seen in figure 8), there fewer census tracts that fall below <-0.5 standard deviations from the mean in 2012 as compared to 2011 (Figures 7 and 8), and there is always the possibility that we may see an increase due to chance as a normal distribution is a probability distribution. There, however, is no way to confirm that there will be an increase without additional data.        

Z-Score Results

	2011	2012
Census Tract 25	-0.61	-.94
Census Tract 108	2	1.48
Census Tract 120.01	1.78	3

Figure 4: Z-Score Results for Selected Tracts, 2011 and 2012 Data

Probability Results

The number of foreclosures exceeded 80% of the time is 3.98 foreclosures, meaning that this number is very likely to be observed in a census tract.

The number of foreclosures exceeded 10% of the time is 24.97 foreclosures, meaning that this number is very unlikely to be observed in a census tract.

   

Figure 5: Changes in Foreclosures Between 2011-2012 in Absolute Values

Figure 8: Foreclosure Totals, 2012 Data

Figure 7: Foreclosures by Census Tract, 2011, Standard Deviation Classification Method

Figure 8: Foreclosures by Census Tract, 2012, Standard Deviation Classification Method

Assignment 2
Goals of Assignment 2
Increase Familiarity with Definitions of Descriptive Statistics
Increase Familiarity with Statistical Methods
Increase Familiarity with Computer Programs

Part 1
Methods: Range, mean, median, mode, kurtosis, skewness, and standard deviation were defined by the author, in his own words. Data supplied by Dr. Ryan Weichelt was used to hand calculate a standard deviation for two sets of data: the first standard deviation was calculated using a sample of student's standardized test scores from Eau Claire North High School and the other standard deviation was calculated using a sample of student's standardized test scores from Eau Claire Memorial. Microsoft Excel was then used to calculate the range, mean, median, mode, kurtosis, skewness, and standard deviation for the Eau Claire North and Eau Claire Memorial data samples. These results were then used to answer the following question; "Should Eau Claire North teachers worry about not having the highest test grade?"

Definitions

Range: The range is the difference between the highest and lowest scores; max score - low score.

Mean: The mean is the calculated average of all observations, found by adding all observations together then dividing by the total number of observations.

Median: The median is the midpoint of the data set; half of the observations fall above and half fall below this point. If the total number of observations is odd, it is simply the middle number in the data set and, if the total number of observations are even, it is the average of the two middle observations.

Mode: The mode is the most frequently occurring data point found in a set of observations.

Kurtosis: Kurtosis (Fig. 1) is the shape of the distribution curve and can be mesokurtic (normal), leptokurtic (peaked), or platykurtic (flat). A value greater than 1 is considered leptokurtic while a value less than -1 is considered platykurtic. Curves that are lepto- or platykurtic have this shape as 68% of the observations one standard deviation above and below the mean have to fit in that area (Fig. 2). Leptokurtic distributions have smaller standard deviations as there are more observations near the mean while platykurtic distributions have larger standard deviation values.

Figure 1: Kurtosis

(http://grants.hhp.coe.uh.edu/doconnor/PEP6305/KurtosisPict.jpg)

Figure 2: Normal Distribution

(http://img.tfd.com/dorland/distribution_normal.jpg)

Skewness: Skewness (Fig. 3) is the measure of the asymmetry of a distribution curve due to a higher-or lower-than-expected number of observations that fall into the positive or negative ends of the curve; if  positive there is an extended tail to the positive side (due to more observations that are lower-than-expected) and, if negative (due to more observations that are higher-than-expected), an extended tail to the negative side. A value below 1 and above -1 is considered normal.

Figure 3:Skewness

(https://www.isobudgets.com/wp-content/uploads/2015/10/skewness.jpg)

Standard Deviation: The standard deviation (Fig. 4) is the distribution/distance of scores about/from the mean, found by subtracting the mean from each observation, squaring the result, then finding the square root of the sum of these results after dividing by N or n-1. In this assignment n-1 was used as this is a sample population standard deviation.

Figure 4: Sample and Population Standard Deviation Equations

(http://dsearls.org/courses/M120Concepts/ClassNotes/Statistics/StandardDeviation2a.gif)

Hand Calculation

Eau Claire North Test Score Data Hand Calculation

Figure 5: Eau Claire North Data

Eau Claire Memorial Test Score Data Hand Calculation

Figure 6: Eau Claire Memorial Data

Results

Eau Claire North Test Scores

Eau Claire Memorial Test Scores

This data suggests that teachers at Eau Claire North have no reason to worry about being fired because their students have lower test scores than students at Eau Claire Memorial. The four  descriptive statistics that are best for determining this are the range, median, mean and kurtosis. I chose these for the simple fact that they portray score differences in a manner that is easy to explain to people with little knowledge of descriptive statistics. EC North students have a lower range (83 compared to 91) which shows us that their test scores are less widely dispersed than the EC memorial students scores were; i.e. the lowest score attained by a student at North (111) was closer to the highest score attained by another student at North (194) than the difference between the lowest (107) and  highest (198) scores attained at Memorial. This may suggest that the North students taking the test were better prepared at all levels of ability as compared to the students at Memorial. The median was higher at North (164.5) than at Memorial (159.5). This tells us that half of the students at North who took this exam in this sample had a score higher than 164.5 and half had a score lower than 164.5, compared to Memorial's median of 159.5. The mean test scores in this sample show that North, with a 160.92 average, had a higher mean test score than Memorial, at 158.54, did. Kurtosis refers to the shape of the distribution; the shape of the distribution curve based on the sample of test scores at North (-.56) is between -1 and 1 and is normal. The shape of the distribution curve based on the test score samples from Memorial is less than -1 (-1.17) and is considered platykurtic. This flatness of the curve is due a larger standard deviation value (27.16) and reflects the extreme disbursement of scores from the mean; we have less scores near the mean score of (158.54) than we observe based on the sample from North (160.92), i.e. the scores at north were closer to the mean. The students at North, on average, performed better on this standardized test. These statistics show that the teachers and students at North are doing quite well and public perceptions are not only unjustified but probably incorrect. This analysis was done using a sample of test scores from both schools using descriptive statistics; we are describing what we see and can make assumptions about this data but we cannot make any inferences regarding it. 

Part 2

Methods: The shapefile used in Assignment 1 was added to a blank map in ArcGIS and a Microsoft Excel spreadsheet, provided by Dr. Ryan Weichelt containing Wisconsin population data by county, was joined to the shapefile based on countyGeo_id. Three spatial statistic analyses were performed: a geographic mean center of Wisconsin (Toolbox/Spatial Statistics/Measuring Geographic Distributions/Mean Center), a weighted mean center of population using 2000 Wisconsin county population data (Toolbox/Spatial Statistics/Measuring Geographic Distributions/Mean Center/Weight/2000), and finally a weighted mean center of population using 2015 Wisconsin county population data (Toolbox/Spatial Statistics/Measuring Geographic Distributions/Mean Center/Weight/2105). 

Mean Center: The mean center is a spatial measurement of central tendency; in the map below it is represented by the red point which represents the geographical center of the state of Wisconsin found by averaging X and Y values (latitude and longitude).

Weighted Mean Center: Weighted mean centers are concerned with the frequencies in data sets; in the map below mean centers were weighted by population. More populous areas (counties) have a higher number of people and therefore have a heavier weight which pulls the geographic mean center toward the direction of more populous counties.

Results: The green point represents the weighted mean center of population in 2000, and the blue, of 2015. Both points are pulled to the southeast of the geographic center of Wisconsin, which is the red point, as the southern and eastern regions of Wisconsin have a higher population than the northern and western parts of the state. This is due to high populations in cities such as Milwaukee (southeast corner of the state), Madison (south-central), and Green Bay (east-central), for example. We observe, however, that the weighted mean center of population in 2015 has been pulled slightly to the southwest of the weighted mean center of population observed in 2000. An explanation for this is slight increase in county populations in the southern and western parts of the state that is greater than the increase in the northern and eastern counties in the state.